Địa điểm của bến phà phải được chọn thế nào để chi phí xây dựng là ít tốn kém nhất?

Ở một khu xây dựng mới có hai nhà máy lớn, vị trí các nhà máy như biểu diễn trên hình vẽ, đặt tại hai điểm A và B. Sản phẩm của các nhà máy phải được vận chuyển đến bờ sông, trên hình vẽ được biểu diễn bằng đường thẳng XY, sau đó đưa lên thuyền và vận chuyển đi nơi khác. Hiện tại người ta chuẩn bị xây dựng trên bờ sông một bến phà, sau đó xây dựng hai con đường từ các nhà máy đến bến phà. Địa điểm của bến phà phải được chọn thế nào để chi phí xây dựng là ít tốn kém nhất?

cách xây bến phà

Vì chi phí xây dựng con đường liên quan trực tiếp đến độ dài của con đường. Để chi phí xây dựng con đường ít tốn kém nhất thì phải chọn để tổng chiều dài của hai con đường ngắn nhất. Như vậy vấn đề đặt ra cho toán học giải quyết là phải chọn một điểm C thế nào cho AC+ BC là ngắn nhất.

Bây giờ ta sẽ dùng các tri thức toán học để giải quyết vấn đề này. Trước hết từ điểm B ta vẽ đường vuông góc với đường thẳng XY, gặp XY tại E. Kéo dài BE một đoạn ED = BE. Nối AD, AD sẽ cắt XY tại điểm C. Dưới đây ta sẽ chứng minh AC + BC là ngắn nhất. Vì B và D đối xứng với nhau qua XY, nên khoảng cách từ B và D đến bất kì điểm nào trên XY cũng bằng nhau (vì XY là đường trung trực của BD). Vì vậy tổng chiều dài của điểm A đến một điểm trên XY và từ điểm đó đến điểm B cũng bằng tổng chiều dài từ điểm A đến XY rồi đến D. Nói cách khác là AC + BC = AD là khoảng cách ngắn nhất từ A đến rồi đến B.
Vì vậy với nhiều vấn đề thực tế nếu chịu khó suy nghĩ, ta có thể vận dụng toán học để giải quyết được.

Tìm hiểu thêm : 

Làm thế nào bạn có thể tạo được một hình chữ nhật hoàn chỉnh ?

Làm thế nào bạn có thể tạo được một hình chữ nhật hoàn chỉnh ?

Giả sử có mảnh ván hình chữ nhật, hình chữ nhật này có hai cạnh song song đã hoàn hảo, hai cạnh đối diện còn lại lại nham nhở, làm thế nào bạn có thể tạo được một hình chữ nhật hoàn chỉnh. Để tạo hình chữ nhật, ta phải cắt đường biên nham nhở theo một đường vuông góc với hai cạnh song song, nhưng lại không có êke. Vậy làm thế nào để vẽ đường thẳng vuông góc với hai đường kia. Ta hãy lấy một chiếc thước có chia độ. Trước hết ta chọn trên đường biên AB một đoạn EF bằng 30 mm như ở hình vẽ. Sau đó dùng E và F làm tâm vẽ hai cung tròn một cung là thuộc đường có tâm tại E bán kính 50 mm và một cung thuộc vòng tròn tâm F bán kính 40 mm. Hai cung tròn sẽ cắt nhau tại điểm G. Nối FG, góc EFG = 90o. Cắt bỏ phần mảnh gỗ ở phía dưới FG ta sẽ có một đường biên hoàn chỉnh của hình chữ nhật. Dùng phương pháp tương tự ta sẽ có được đường biên phía trên hoàn chỉnh.

Thế tại sao ta khẳng định EFG =90o. Bởi vì tỉ số các cạnh EF : FG: EC = 3 : 4: 5 đây là tam giác đồng dạng với tam giác vuông có ba cạnh 3, 4, 5 trong cạnh dài EG đối diện với góc vuông EFG.

Bây giờ nếu thước chia độ cũng không có thì ta sẽ làm thế nào?
Chúng ta sẽ chọn một thanh gỗ tương đối thẳng, dùng bút chì đánh dấu hai điểm M, N trên thanh gỗ (như hình vẽ). Sau đó đặt thanh gỗ trên tấm gỗ, đặt điểm M ở mép tấm gỗ. Dùng bút chì đánh dấu hai điểm P và Q ngay ở các vị trí M và N trên tấm gỗ.

Sau đó thay đổi phương của thanh gỗ. Giữ cho điểm N bất động. Cho điểm M di động trên biên của tấm gỗ. Dưới điểm M ta đánh dấu điểm R. Kéo dài RQ, trên phần kéo dài ta đặt QS = MN. Nối PS, góc RPS =90o. Dùng phương pháp đơn giản như vừa mô tả ta vẽ được đường vuông góc, cắt tấm gỗ theo đường vuông góc vừa vẽ, ta sẽ có một cạnh hình chữ nhật.
Để chứng minh RPS là góc vuông, ta nối PQ. Vì RQ = PQ = QS

nên các tam giác RQP và SQP là những tam giác cân. Do đó: RPS = RPQ + QPS =PRQ + QSP

Vì các góc RPS,PRS,RSP là các góc trong của tam giác RPS, tổng của chúng là 180o, vì vậy góc = 90o.

Về vấn đề này nhà toán học Trung Quốc Hoa La Canh đã từng bàn đến. Điều này hoàn toàn hiển nhiên đối với hình vuông hoặc hình chữ nhật. Nhưng đối với một tứ giác bất kì thì liệu điều đó có chính xác không?

Xét một tứ giác ABCD bất kì, các đoạn nối các điểm giữa các cạnh là EG và FH cắt nhau tại P, P sẽ là trung điểm của EG và FH. Ta hãy tưởng tượng có 4 quả cầu nhỏ đặt tại các đỉnh A, B, C, D, mỗi quả cầu cho 1 lực tác dụng là 10N (N: đơn vị đo lực, đọc là niutơn). Hợp lực của hai quả cầu đặt tại A, B sẽ cho hợp lực tác dụng tại điểm E, hợp lực tác dụng khoảng trên dưới 20 N; các quả cầu nhỏ C, D cho hợp lực đặt tại điểm G có giá trị gần 20 N. Như vậy bốn quả cầu sẽ cho hợp lực đặt tại trung điểm của EG là đường nối các trung điểm với hợp lực gần 40 N. Cùng lí do tương tự, bốn quả cầu cũng cho hợp lực tác dụng tại trung điểm của FH gần 40 N. Như vậy bốn quả cầu sẽ cho hợp lực tác dụng tại trung điểm của EG và FH là điểm duy nhất và điểm P là trung điểm của EG và FH.

Lại giả sử ta dùng kéo cắt tứ giác theo các đường EG, FH thành bốn mảnh và lấy các điểm H, G, F làm bản lề, kéo căng các mảnh để AH trùng với DH và DG trùng với CG. Do tổng bốn góc trong của tứ giác là 360o, nên . Lúc cạnh AE của mảnh I trùng với cạnh BE của mảnh thứ II, dễ thấy là lúc bấy giờ ta lại nhận một hình tứ giác mới là một hình bình hành, mà các cạnh đối từng đôi bằng tổng của EG + FH, và bốn góc trong là các góc kề bù nhau. Diện tích hình bình hành mới này rõ ràng bằng diện tích của hình tứ giác cũ nên:

Trong biểu thức ở trên dấu = chỉ xuất hiện khi

Vì vậy tích của hai đường nối các trung điểm rõ ràng lớn hơn diện tích của tứ giác.

Bài khác : 

Ngôi sao năm cánh

Từ khoá: Hình tứ giác và diện tích.

Ngôi sao năm cánh

Ngôi sao năm cánh là loại hình vẽ mà mọi người khá quen thuộc.
Thế nhưng bạn có biết cách vẽ chính xác một ngôi sao năm cánh? Dưới đây chúng tôi xin giới thiệu một phương pháp vẽ ngôi sao năm cánh chính xác.
Vẽ một vòng tròn tâm O.
Vẽ hai đường kính của vòng tròn AZ và XY vuông góc với nhau.
Chọn M là điểm giữa của OY.
Lấy M làm tâm, MA làm bán kính, vẽ cung tròn AN, cung tròn cắt OX tại điểm N.
Lấy A làm tâm, MA làm bán kính cắt trên vòng tròn các cung tròn liên tiếp bằng nhau: AB = BC = CD = DE = EA.
Nối liên tiếp các đỉnh AD, AC, EB, EC, BD, ta đã vẽ xong ngôi sao năm cánh.
Dưới đây ta sẽ chứng minh tính chính xác của cách vẽ vừa trình bày. Cho vòng tròn có bán kính R. Từ cách vẽ trên đây ra thấy:

AN² = AO² + ON² = AO² + (AM - OM)²

Vì vậy

Nếu quả hình ngôi sao vừa vẽ là chính xác thì năm đỉnh của ngôi sao phải nội tiếp trong vòng tròn bán kính R. Nói khác đi, ta phải chứng minh AN chính bằng độ dài cạnh của ngũ giác đều nội tiếp trong bán kính vòng tròn ngoại tiếp của ngôi sao năm cánh.
Theo các kiến thức đã học ở bậc trung học, ta biết cạnh của hình thập giác đều nội tiếp trong hình tròn bán kính R sẽ bằng

a10 = ¹/2 (√5 - 1)R

a10 

là độ dài cạnh của thập giác đều nội tiếp trong vòng tròn bán kính R.
Dưới đây ta sẽ tính cạnh của ngũ giác đều nội tiếp trong vòng tròn bán kính R. Giả sử DZ = ZC = a10 là cạnh của thập giác đều nội tiếp còn DC = a5 là cạnh của ngũ giác đều nội tiếp.
Tam giác cân ODZ có diện tích

Rõ ràng là AN = a5. 

Vì vậy phương pháp ta vẽ ngôi sao năm cánh trình bày ở trên là chính xác.

Không phải bất kì đa giác đều nào nội tiếp trong vòng tròn đều có thể vẽ được bằng thước và compa. Các hình tam giác đều, ngũ giác đều, thập giác đều cũng như các đa giác đều có nguồn gốc trực tiếp từ chúng như các hình có số cạnh 2n, 2n x 3, 2n x 5, 2n x 15 (n là số dương) là những đa giác đều mà từ hơn 2000 năm về trước vào thời đại Ơclit người ta đã biết. Từ đó rất nhiều năm sau chưa hề có bước đột phá nào, mãi đến thế kỉ XVIII Gauss mới lần đầu tiên tìm ra cách

vẽ đa giác 17 cạnh. Có thể phán đoán: một đa giác đều n cạnh thì n = 2^m. P1. P2...P mới có thể vẽ được bằng thước và compa. Trong đó

P1, P2...P là các số 2^2k+1, m là số dương bất kì hoặc bằng 0. Lời dự đoán trên đây do Gauss đưa ra và đã cùng chứng minh với một nhà toán học khác.

 

Bạn đọc thêm : 

Bàn Thất Xảo

Từ khoá: Hình nhiều cạnh.

Bàn Thất Xảo

Bàn thất xảo là loại bàn dã chiến lắp ghép từ năm hình tam giác (hai hình lớn, hai hình nhỏ, một hình kích thước trung bình), một hình bình hành, một hình vuông, tất cả là bảy tấm ghép, ghép lại mà thành. Như ở hình 7 tấm ghép đã ghép nối lại thành một hình vuông. Giả sử chúng ta chọn để bàn hình vuông được ghép lại có cạnh bằng bốn, chúng ta có thể tính toán kích thước của mỗi mảnh ghép. Bảng mảnh ghép sẽ có 5 x 3 + 4 + 4 = 23 đường biên. Độ dài của mỗi đường biên sẽ có 4 loại: 2, 4,√2 và 2√2 . Vả lại 2√2 và 4 là gấp đôi của √2 và 2 nên chiều dài của các mảnh ghép của bàn thất xảo thực tế chỉ có hai loại. Chính vì vậy từ các mảnh dễ dàng lắp ghép thành các loại bàn có hình dạng khác nhau.

Loại bàn thất xảo đã xuất hiện ở Trung Quốc hơn ngàn năm trước, vào thời đó bàn thất xảo mang tên là “Kỉ yến” bàn tiệc, là một loại bàn chân thấp sử dụng khi bày các bàn tiệc. Điều lí thú là mỗi chiếc bàn lắp ghép theo các quy cách khác nhau sẽ có kích thước nhất định chọn trước, tháo rời ra lại có thể sử dụng riêng biệt. Khi có đông khách, tuỳ theo nhu cầu có thể làm mặt bàn ghép lại kích thước to hơn, mặt bàn có thể biến đổi nhanh chóng. Vì vậy được mọi người ưa thích. Vào thời Tống loại bàn tiệc chỉ có sáu mảnh, sau này mới thêm một mảnh nữa thành bảy.

Bàn thất xảo có từ các buổi yến tiệc, sau này lan truyền ra nước ngoài và được gọi là “bàn Nhà Đường”. Bàn thất xảo được lưu truyền cho đến ngày nay vì chỉ với bảy mảnh gỗ có thể sắp xếp thành nhiều kiểu mặt bàn khác nhau, hơn nữa với cùng một kiểu mặt bàn lại có thể được lắp ghép theo nhiều cách khác nhau.

Thế nhưng diện tích lớn nhất của bàn thất xảo có thể thu được là bao nhiêu? Ta thử tính xem. Hai tam giác nhỏ, mỗi hình chỉ có diện tích bằng 1. Diện tích hình tam giác trung bình, diện tích hình bình hành và diện tích hình vuông do hai tam giác nhỏ ghép lại, diện tích của chúng là 2. Hai hình tam giác lớn có diện tích bằng 4. Hình tam giác lớn có thể do hai hình tam giác nhỏ ghép với hình bình hành; cũng có thể do hai tam giác nhỏ và hình vuông ghép lại, lại cũng có thể do hai tam giác nhỏ ghép với tam giác trung bình. Diện tích của bảy mảnh ghép sẽ là:

1 + 1 + 2 + 2 + 2 + 4 + 4 = 16, đó cũng chính là diện tích lớn nhất mà bàn thất xảo cho phép lắp ghép được.
Bạn hãy thử xem với bàn thất xảo bạn có thể thu được bao nhiêu kiểu mặt bàn?
Bạn đọc thêm : 
Tại sao các vách ngăn của tổ ong tạo thành hình lục giác ?

Từ khoá: Bàn thất xảo.

Tại sao các vách ngăn của tổ ong tạo thành hình lục giác ?

Nếu quan sát kĩ các tổ ong, bạn sẽ thấy có nhiều điều đáng kinh ngạc. Kết cấu của tổ ong quả là kì tích trong tự nhiên. Các tổ ong ở do nhiều tấm vách ngăn có độ lớn nhỏ giống nhau tạo thành, nhưng nhìn từ chính diện chúng đều là hình sáu cạnh, sắp xếp đều đặn.

Kết cấu tổ ong

Nhưng nếu nhìn nghiêng thì đó là các hình lăng trụ lục giác sắp xếp khít nhau. Nhưng đáy của các lăng trụ lại làm cho người ta kinh ngạc hơn! Các đáy không bằng cũng không phải là mặt hình tròn, cũng không nhọn mà là do ba hình thoi hoàn toàn đồng nhất ghép lại thành một đáy nhọn.

Dạng lục giác kì diệu của các tổ ong gợi sự chú ý của nhiều người. Tại sao các vách ngăn của tổ ong tạo thành hình lục giác mà không tạo thành hình tam giác, hình vuông, hình ngũ giác.

Vì các vật thể hình lăng trụ khi chịu áp lực bốn bên: trái, phải, trước, sau tiết diện sẽ biến thành hình lục giác đều. Vì vậy theo quan điểm lực học, hình lục giác là hình có tính ổn định cao nhất. Thế khi ong xây tổ có phải chúng đã bị loại sức ép như vậy tác động? Đương nhiên không phải như vậy.

Hình lục giác của tổ ong ngay từ đầu đã liền phiến như vậy.

Vào thế kỉ XVIII, một học giả người Pháp là Moralti đã tiến hành đo đạc cẩn thận các góc trong tổ ong và phát hiện ra một quy luật lí thú: Các hình thoi ở mặt đáy của tổ ong có góc tù là 109o28' còn góc

nhọn là 70o32'. Hiện tượng này gợi ý cho nhà vật lí Reaumur liệu đó có phải là giải pháp xây tổ ong cho phép tiết kiệm nguyên liệu nhất mà dung tích chỗ ở lại lớn nhất? Do đó ông đã trao đổi ý kiến với nhà toán học Thuỵ sĩ là Koenig. Qua tính toán cẩn thận, Koenig đã khẳng định các phán đoán của Reaumur. Thế nhưng theo các tính toán chính xác của Koenig thì các góc của hình thoi phải là 109o26' và 70o34', so với các số liệu đo đạc ở tổ ong thời đó thì sai khác hai phút.

Vào năm 1743, nhà toán học Anh là Maclaurin lại nghiên cứu cấu trúc tổ ong. Ông đã dùng một phương pháp mới tính toán và đi đến kết luận là các góc trong tổ ong hoàn toàn phù hợp với các kết quả tính toán. Nguyên do của sai lệch đã nêu trên là do Koenig đã dùng một bảng số in sai.

Qua mấy thế kỉ nghiên cứu cấu trúc tổ ong, cuối cùng người ta tìm thấy là chính cấu trúc tổ ong hữu hiệu nhất về mặt tiết kiệm nguyên liệu và không gian. Ngoài ra người ta còn tìm thấy loại cấu trúc này còn có nhiều tính năng kì diệu khác. Ngày nay kiểu cấu trúc tổ ong được ứng dụng nhiều trong kiến trúc, trong hàng không và vô tuyến điện thoại. Các kết cấu “tầng tổ ong” có lợi về mặt cách nhiệt, cách âm trong kiến trúc, cũng như trong thiết kế các ống thoát khí cho các động cơ hàng không.
Tìm hiểu thêm : 

Có bao nhiêu cách lắp ghép các mảnh khảm gồm các hình nhiều cạnh ?

Từ khoá: Kết cấu tổ ong; Hình lục giác; Lăng trụ lục giác đều.

Có bao nhiêu cách lắp ghép các mảnh khảm gồm các hình nhiều cạnh ?

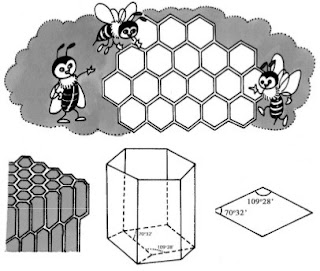
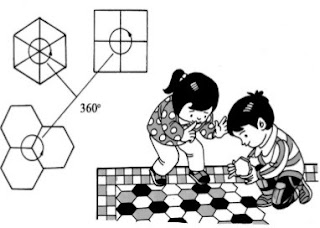
Bạn có chú ý trong đời sống hàng ngày có bao nhiêu loại hình khảm, đó là các mảnh hình khảm ghép lại với nhau mà thành.

Yêu cầu của các hình khảm là khi các đường chu vi gặp nhau tổng các góc phải bằng 360o, nhờ vậy khi ghép chúng lại sẽ không có khe hở. Nếu dùng các mảnh khảm gồm các hình nhiều cạnh thì có bao nhiêu cách lắp ghép?

Trước hết xem xét từ khía cạnh các điểm gặp nhau của các hình có nhiều cạnh. Do các góc trong của các đa giác nhỏ nhất là 60o, lớn

nhất là 180o nên chỉ có các hình 3, 4, 5, 6 cạnh là có thể sử dụng. Ta thử xét ba tình huống. Ta gọi các hình đa giác có các số cạnh là x, y, z thì các góc trong sẽ là:

Khi ghép chúng lại với nhau để khảm thì : 

Bởi vì 1/x + 1/y + 1/z = 1/2

Không kể trật tự sắp xếp của các số x, y, z thì phương trình này có 10 nhóm nghiệm là:



(3, 7, 42); (3, 8, 24); (3, 9, 18); (3, 10, 15); (3, 12, 12); (4, 5, 20); (4,

6, 12); (4, 8, 8); (5, 5, 10); (6, 6, 6).



Cũng với lí luận tương tự khi chọn phương án bốn loại đa giác ta có bốn nhóm nghiệm: (3, 3, 4, 12); (3, 3, 6, 6); (3, 4, 4, 6); (4, 4, 4, 4).

Với phương án năm loại đa giác sẽ có hai nhóm nghiệm (3, 3, 3, 3, 6) và (3, 3, 3, 4, 4), còn nếu dùng sáu loại đa giác thì chỉ có một nhóm nghiệm (3, 3, 3, 3, 3, 3).

Như vậy nếu xét theo quan điểm, điểm giao nhau của các đa giác đều có 17 loại cách phối trí khác nhau. Thế nhưng có phải cả 17 phương án này đều có thể sử dụng trong kĩ thuật nạm khảm. Thực tế chỉ có các đa giác đều có 3, 4, 6, 8, 12 cạnh là có thể ghép nối vào nhau để khảm làm 11 loại khảm ghép để lấp kín bề mặt mà không có khe hở, còn sáu loại đa giác khác chưa tìm được cách ghép thành công.

Thế thì từ 11 loại tình huống có thể có cách sắp xếp nào? Chúng ta có thể bàn đến bốn loại sắp xếp chính:

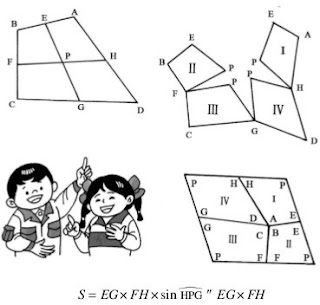
Các hình khảm đều: Tức là dùng cách lắp ghép các đa giác cùng loại như ở các hình vẽ 1 - 3. Chỉ có 3 loại lắp ghép (6, 6, 6); (4, 4, 4, 4) và (3, 3, 3, 3, 3).

Các hình khảm nửa đều: Dùng cách lắp ghép các hình đa giác không đồng nhất nhưng số điểm giao nhau của đường biên các đa giác đều giống nhau như ở các hình vẽ từ 4 - 9. Có 6 loại (3, 12, 12); (4, 8, 8); (3, 3, 6, 6); (3, 4, 4, 6); (3, 3, 3, 6) và (3, 3, 3, 4, 4).

Các hình khảm đều đặn: Số giao điểm của các đường biên các đa giác là giống nhau, chỉ có thứ tự sắp xếp khác nhau như ở các hình vẽ 10 - 13. Loại khảm này dựa vào giao điểm các đường biên của các đa giác theo một thứ tự nhất định, nhưng vị trí tương đối của các giao điểm là vô hạn. Ví dụ nếu dịch chuyển ô giữa của hình 11 sang bên phải một ô ta sẽ có một loại đồ hình khảm khác. Nếu cách 1, 2, 3... hàng di chuyển sang phải một ô sẽ được một hình khảm khác. Vì vậy ở hình khảm này ta sẽ thu được nhiều loại.

Các hình khảm không đều đặn: Các giao điểm của các đường biên của các đa giác không giống nhau, số giao điểm cũng không giống nhau. Các hình khảm này cũng có vô số loại.

Ngoài các phương án kể trên người ta có thể sử dụng các hình tam giác, hình bốn cạnh không đều hoặc các đường gấp khúc, cũng nhận được các hình khảm tinh xảo.

Bạn đọc thêm : 

Cách ghép các mảnh gỗ hình tứ giác với nhau ?

Từ khoá: Hình khảm; Hình đa giác đều.

Cách ghép các mảnh gỗ hình tứ giác với nhau ?

Chúng ta sau khi đã học xong một định lí toán học, thì nên chú ý liên hệ chúng với thực tiễn cuộc sống, sản xuất. Hãy xem xét một ví dụ sau.

Trong một nhà máy có một đống phế liệu, trong đó có nhiều tấm gỗ hình 4 cạnh, các tấm gỗ phế liệu này có kích thước hoàn toàn giống nhau dù hình dáng có khác nhau: có tấm hình vuông, có tấm chữ nhật, đều là các hình 4 cạnh khác nhau. Nếu đem chúng xử lí và chế tác thành những hình có quy củ thì sẽ cắt bỏ nhiều mảnh nhỏ vụn, lãng phí gỗ. Nhiều người đã tính toán tìm cách tận dụng thật tốt phế liệu.

Sau này có người dùng các gỗ phế liệu này để phủ sàn nhà, nhờ vậy bất kể các tấm lớn nhỏ đều có thể tận dụng làm ván sàn, chỉ cần gia công hai đầu chút ít là được.

Tại sao vậy? Vì tổng các góc trong của các tứ giác đều là 360o.

Theo các lí do như trên ta có thể cắt để lắp kín mặt bằng không có khe hở. Theo cách này, ta có thể chế tác các tấm gỗ thành băng dài, đương nhiên cũng có thể ghép chúng thành mảng có kích thước lớn.

Nhờ vậy có thể sử dụng các tấm gỗ hình bốn cạnh bất kì ghép thành tấm phủ mặt đất.

Dùng máy tính điện tử người ta có thể tìm được nhiều phương án lắp ghép trước nay chưa từng có.

Bạn đọc thêm : 

Tại sao gạch lát nhà đều có dạng hình vuông hoặc hình lục giác ?

Từ khoá: Hình nhiều cạnh.

Tại sao gạch lát nhà đều có dạng hình vuông hoặc hình lục giác ?

Gạch hoa lát nhà có nhiều loại nhưng nói chung đều có dạng hình vuông hoặc hình lục giác. Tại sao vậy?

Trong các hình phẳng nhiều cạnh đều chỉ có ba loại hình có thể lắp kín một mặt phẳng không có khe hở là các hình tam giác, hình vuông và hình lục giác. Với hình tam giác đều có ba góc đều bằng 60o, khi ghép sáu hình tam giác đều lại với nhau ta sẽ có một đỉnh chung là 360o. Hình vuông có mỗi góc là 90o, ghép bốn hình vuông với nhau, ta cũng có một đỉnh chung là 360o. Với hình lục giác có các góc là 120o, khi ghép ba lục giác lại với nhau ta cũng thu được một hình có đỉnh chung là 360o.

Nếu dùng các hình nhiều cạnh đều khác thì không đạt được yêu cầu đó. Ví dụ nếu dùng hình ngũ giác đều chẳng hạn. Mỗi góc của hình ngũ giác đều là 180o. Nếu ghép ba ngũ giác lại với nhau, ta sẽ có

đỉnh chung là 324o, nhỏ hơn 360o nên có khe hở. Nếu dùng bốn hình ngũ giác ghép lại với nhau thì có góc chung là 108o x 4 = 432o lớn hơn 360o.

Ghép các hình tam giác đều với nhau tuy không có khe hở nhưng gạch hoa có hình tam giác thì trông không đẹp bằng hình vuông hoặc hình lục giác đều. Nên trong nghệ thuật thiết kế người ta hay dùng các hình vuông hoặc hình lục giác.

Bài viết khác : 

Luyện tầm nhìn thiên lí - Dấn thêm một tầng lầu như thế nào?

Từ khoá: Hình vuông, hình tam giác đều, hình lục giác đều.

Luyện tầm nhìn thiên lí - Dấn thêm một tầng lầu như thế nào?

Nhà thơ nổi tiếng thời Đường là Vương Chi Hoán, trong bài thơ “Lên lầu quán tước”1 đã viết:

Mặt trời đà gác núi Hoàng hà nhập biển khơi Luyện tầm nhìn thiên lí Dấn thêm một tầng lầu.

Trong bài thơ có nói “thiên lí” là cách nói khoa trương, ý nói là có tầm nhìn xa. Thế nhưng nếu bạn có hứng thú bạn thử tưởng tượng để có tầm nhìn thiên lí - tầm nhìn ngàn dặm (500 km) ta thử xem phải lên toà nhà có bao nhiêu tầng, cao bao nhiêu?

Theo như hình vẽ, giả sử đại diện cho mặt đất, 0 là trung tâm Trái Đất, C là điểm cách A 500000 m, dĩ nhiên người đứng tại điểm A sẽ không nhìn thấy điểm C, mà muốn nhìn thấy điểm C thì bắt buộc phải từ điểm B ở xa mặt đất. Tia nhìn BC có liên quan chặt chẽ với cung AC, AB chính là tầng lầu có chiều cao thấp nhất mà đứng từ đó có thể quan sát thấy điểm C.

Vì AB = OB - OA, OA là bán kính Trái Đất và bằng 6370 km, nên để tính AB ta chỉ cần tính OB.

Trong tam giác vuông OCB

Và

AB = OB - OA = 6390 km - 6370 km = 20 km

Từ các tính toán cho thấy ít nhất thì toà lâu đài cũng cao đến 20 km, cao hơn đỉnh núi cao nhất thế giới là đỉnh Chômôlungma (tức đỉnh Evrest) nhiều. Tầng lầu cao đến như vậy quả là chưa từng có.

Bài mới nhất : 

Làm thế nào để đo được chiều cao của Kim tự tháp?

Từ khoá: Tầm nhìn thiên lí.

Làm thế nào để đo được chiều cao của Kim tự tháp?

Các bạn có biết các Kim tự tháp Ai Cập không? Kim tự tháp là các công trình kiến trúc hùng vĩ cổ Ai Cập, là các phần mộ của các quốc vương cổ ai cập.

Vào hơn 2600 năm trước có một quốc vương Ai Cập, muốn biết Kim tự tháp lớn có độ cao chính xác là bao nhiêu, thế nhưng không có ai biết được phải đo độ cao Kim tự tháp như thế nào.

Cho người bò lên đỉnh tháp, không thể làm được. Bởi vì tháp có độ nghiêng nên cho dù có thể bò lên đến đỉnh thì đo bằng phương pháp nào?

đo chiều cao kim tự tháp

Về sau vị quốc vương mời một học giả nổi tiếng là Fares để giải quyết vấn đề này. Fares đã chọn một ngày đẹp trời, với sự có mặt của quốc vương và các thày tư tế, Fares bắt đầu đo chiều cao của tháp.

Người xem rất đông đảo, náo nhiệt, người ta vừa xô đẩy vừa tranh luận. Thời giờ đã không còn sớm nữa, Mặt trời đã lên cao khiến cho bóng người và bóng tháp đã khá dài. Khi Fares đã biết thời điểm mà độ dài của bóng của chính mình bằng độ cao thực của mình, ông ra lệnh đo chiều dài của tháp. Bấy giờ các trợ thủ đã đo được chiều dài của bóng tháp có độ dài là DB. Nhờ vào DB, Fares đã đo được độ cao chính xác của tháp.

Bấy giờ mọi người mới hết sức thán phục về sự thông minh của Fares.

Fares quả là đáng nể vì từ hơn 2000 năm trước ông đã biết ứng dụng định lí hình đồng dạng để đo độ cao của Kim tự tháp. Còn môn hình học Ơclid mà chúng ta học ngày nay được Ơclid sáng lập sau Fares nhiều năm.

Thế Fares làm thế nào đo được chiều cao Kim tự tháp? Vì Fares chờ cho chính lúc bóng của mình đúng bằng chiều cao của mình mới bắt đầu đo chiều cao của tháp. Đó là thời điểm mà ánh sáng Mặt trời chiếu nghiêng đúng một góc bằng 45o xuống mặt đất.

Tức:

Góc CBA = 45o Góc ACB = 90o Góc BAC = 45o

Vào thời điểm đó, đỉnh tháp, tâm của đáy tháp và điểm mút của bóng tháp tạo thành tam giác vuông cân và hai cạnh bên AC và CB phải bằng nhau AC = CB. Fares dễ dàng đo được độ dài của đáy tháp. Độ dài một nửa cạnh bên là CD và DB đã đo được; chiều cao của tháp sẽ bằng:

AC = CD + DB
Tìm hiểu thêm : 

Làm thế nào để đo được bề rộng một con sông lớn?

Từ khoá: Hình đồng dạng.